When two parallel lines are given in a figure, there are two main areas: the interior and the exterior.
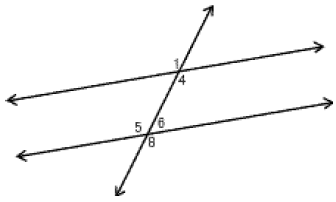
When two parallel lines are cut by a third line, the third line is called the transversal. In the example below, eight angles are formed when parallel lines m and n are cut by a transversal line, t.
There are several special pairs of angles formed from this figure. Some pairs have already been reviewed:
Vertical pairs:
1 and 4
2 and 3
5 and 8
6 and 7
Recall that all pairs of vertical angles are congruent.
Supplementary pairs:1 and 2
2 and 4
3 and 4
1 and 3
5 and 6
6 and 8
7 and 8
5 and 7
Recall that supplementary angles are angles whose angle measure adds up to 180°. All of these supplementary pairs are linear pairs. There are other supplementary pairs described in the shortcut later in this section. There are three other special pairs of angles. These pairs are congruent pairs.
Alternate interior angles two angles in the interior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate interior angles are non-adjacent and congruent.
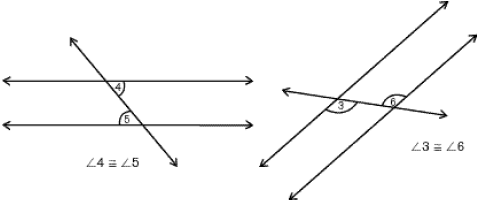
Alternate exterior angles two angles in the exterior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate exterior angles are non-adjacent and congruent.
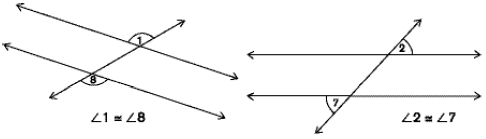
Corresponding angles two angles, one in the interior and one in the exterior, that are on the same side of the transversal. Corresponding angles are non-adjacent and congruent.
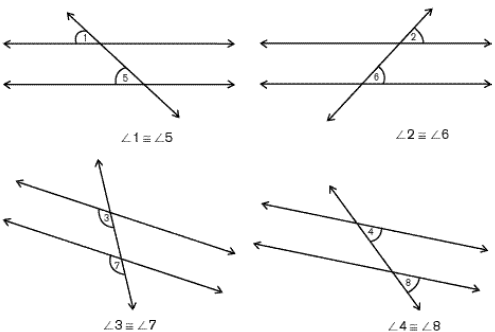
Use the following diagram of parallel lines cut by a transversal to answer the example problems.
Example:
What is the measure of8?
The angle marked with measure 53° and8
are alternate exterior angles. They are in the exterior, on opposite
sides of the transversal. Because they are congruent, the measure of 8 = 53°.
Example:
What is the measure of7?
8 and 7 are a linear pair; they are supplementary. Their measures add up to 180°. Therefore, 7 = 180° – 53° = 127°.
1. When a transversal cuts parallel lines, all of the acute angles formed are congruent, and all of the obtuse angles formed are congruent.
In the figure above1, 4, 5, and 7 are all acute angles. They are all congruent to each other. 1 ≅ 4 are vertical angles. 4 ≅ 5 are alternate interior angles, and 5 ≅ 7 are vertical angles. The same reasoning applies to the obtuse angles in the figure: 2, 3, 6, and 8 are all congruent to each other.
2. When parallel lines are cut by a transversal line, any one acute angle formed and any one obtuse angle formed are supplementary.
From the figure, you can see that3 and 4 are supplementary because they are a linear pair.
Notice also that3 ≅ 7, since they are corresponding angles. Therefore, you can substitute 7 for 3 and know that 7 and 4 are supplementary.
Example:
In the following figure, there are two parallel lines cut by a transversal. Which marked angle is supplementary to1?
The angle supplementary to1 is 6. 1
is an obtuse angle, and any one acute angle, paired with any obtuse
angle are supplementary angles. This is the only angle marked that is
acute.
When two parallel lines are cut by a third line, the third line is called the transversal. In the example below, eight angles are formed when parallel lines m and n are cut by a transversal line, t.
There are several special pairs of angles formed from this figure. Some pairs have already been reviewed:
Vertical pairs:
1 and 42 and 35 and 86 and 7Recall that all pairs of vertical angles are congruent.
Supplementary pairs:
1 and 22 and 43 and 41 and 35 and 66 and 87 and 85 and 7Recall that supplementary angles are angles whose angle measure adds up to 180°. All of these supplementary pairs are linear pairs. There are other supplementary pairs described in the shortcut later in this section. There are three other special pairs of angles. These pairs are congruent pairs.
Alternate interior angles two angles in the interior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate interior angles are non-adjacent and congruent.
Alternate exterior angles two angles in the exterior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate exterior angles are non-adjacent and congruent.
Corresponding angles two angles, one in the interior and one in the exterior, that are on the same side of the transversal. Corresponding angles are non-adjacent and congruent.
Use the following diagram of parallel lines cut by a transversal to answer the example problems.
Example:
What is the measure of
8?The angle marked with measure 53° and
8
are alternate exterior angles. They are in the exterior, on opposite
sides of the transversal. Because they are congruent, the measure of 8 = 53°.Example:
What is the measure of
7?8 and 7 are a linear pair; they are supplementary. Their measures add up to 180°. Therefore, 7 = 180° – 53° = 127°.1. When a transversal cuts parallel lines, all of the acute angles formed are congruent, and all of the obtuse angles formed are congruent.
In the figure above
1, 4, 5, and 7 are all acute angles. They are all congruent to each other. 1 ≅ 4 are vertical angles. 4 ≅ 5 are alternate interior angles, and 5 ≅ 7 are vertical angles. The same reasoning applies to the obtuse angles in the figure: 2, 3, 6, and 8 are all congruent to each other.2. When parallel lines are cut by a transversal line, any one acute angle formed and any one obtuse angle formed are supplementary.
From the figure, you can see that
3 and 4 are supplementary because they are a linear pair.Notice also that
3 ≅ 7, since they are corresponding angles. Therefore, you can substitute 7 for 3 and know that 7 and 4 are supplementary.Example:
In the following figure, there are two parallel lines cut by a transversal. Which marked angle is supplementary to
1?The angle supplementary to
1 is 6. 1
is an obtuse angle, and any one acute angle, paired with any obtuse
angle are supplementary angles. This is the only angle marked that is
acute.
No comments:
Post a Comment